There are many areas of bandwidth application, which can be used to identify the data transmission capability of the signal transmission, identify the amount of data passing through the link in a unit time, and identify the display capability of the display.
1. The analog signal system, also called bandwidth, refers to the amount of data that can be transmitted at a fixed time, that is, the ability to transmit data in the transmission pipeline. It is usually expressed in terms of transmission cycles per second or hertz (Hz).
2. In digital devices, bandwidth refers to the amount of data that can pass through the link per unit of time. It is usually expressed in bps, which is the number of bits that can be transmitted per second.
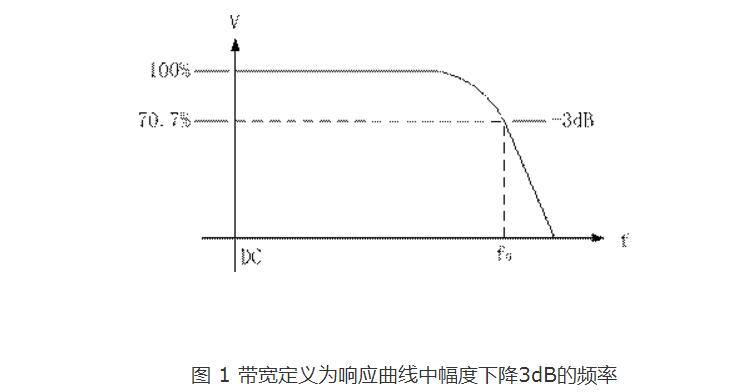
Oscilloscope bandwidthThe oscilloscope bandwidth refers to the input of a signal with the same amplitude and frequency change. When the oscilloscope reading is attenuated by 3dB from the true value, the frequency at this time is the bandwidth of the oscilloscope. In other words, the input signal has a true value of -3dB at the oscilloscope's bandwidth. The bandwidth is not the highest frequency that the oscilloscope can display. In general, the oscilloscope bandwidth should be 3 to 5 times the highest frequency of the measured signal.
For electronics engineers who often deal with oscilloscopes, the oscilloscope's bandwidth is undoubtedly one of their most concerned indicators. Bandwidth directly affects the fidelity of the signal and the accuracy of the measurement. The bandwidth we usually refer to refers to the -3dB bandwidth, as shown in Figure 1. When 200M sine wave is input on a 200M bandwidth oscilloscope, its amplitude will theoretically decrease by 3dB. However, if you divide the amplitude of the signal measured at this time by 0.707, and you want to obtain the amplitude of the real signal, the result obtained may not be correct. Because in practice, when the oscilloscope is designed, in order to ensure the bandwidth parameters and reduce the signal distortion, the signal attenuation in the band is usually less than 3dB. Therefore, the 200M bandwidth is a design indicator, which ensures that the attenuation of the sine wave amplitude within 200M does not exceed 3 dB to provide better measurement confidence.
Sampling frequency, also known as sampling speed or sampling rate, defines the number of samples per second that are extracted from a continuous signal and make up a discrete signal. It is expressed in Hertz (Hz). The reciprocal of the sampling frequency is the sampling period or sampling time, which is the time interval between sampling. The popular sampling frequency refers to how many signal samples the computer collects per second.
Sampling theoremThe so-called sampling theorem, also known as the Shannon sampling theorem, Nyquist sampling theorem, is an important basic conclusion in the information theory, especially the communication and signal processing disciplines.
Sampling is the conversion of a signal (that is, a continuous function of time or space) into a sequence of values ​​(that is, discrete functions in time or space). The sampling theorem states that if the signal is band-limited and the sampling frequency is higher than twice the signal bandwidth, the original continuous signal can be completely reconstructed from the sampled samples.
The speed of the band-limited signal transformation is limited by its highest frequency component, which means that its discrete-time sampling ability to represent the signal details is limited.
The sampling theorem means that if the signal bandwidth is less than half of the sampling frequency (ie Nyquist frequency), then these discrete sample points can fully represent the original signal. Frequency components above or at the Nyquist frequency can cause aliasing. Most applications require avoidance of aliasing. The severity of the aliasing problem is related to the relative strength of these aliasing frequency components.
The sampling frequency must be greater than twice the bandwidth of the sampled signal. Another equivalent argument is that the Nyquist criterion must be greater than the bandwidth of the sampled signal. If the bandwidth of the signal is 100Hz, the sampling frequency must be greater than 200Hz in order to avoid aliasing. In other words, the sampling frequency must be at least twice the frequency of the largest frequency component in the signal, otherwise the original signal cannot be recovered from the signal sampling.
In analog video systems, the sampling rate is defined as the frame rate and field frequency, not the conceptual pixel clock. The image sampling frequency is the cycle speed of the sensor integration period. Since the integration period is much less than the repetition time, the sampling frequency may be different from the reciprocal of the sampling time.
50Hz-PAL video
60/1.001Hz-NTSC Video
When analog video is converted to digital video, another different sampling process occurs, this time using pixel frequencies. Some common pixel sampling rates are:
13.5MHz-CCIR601, D1video
The aliasing phenomenon of the high-frequency luminance component appears as a moiré pattern.
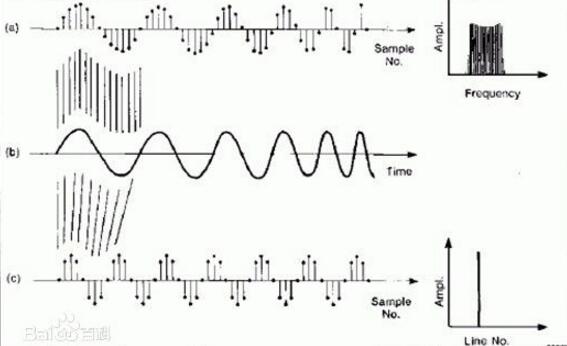
Bandwidth reflects the frequency of the signal through the ability, the greater the bandwidth, the various frequency components in the signal (especially high-frequency components) can accurately enlarge and display, it is more accurate, if the bandwidth is not enough, it will lose a lot of high Frequency components, the signal naturally shows inaccurate, there is a large error. The sampling rate is the frequency at which the signal is converted when the analog quantity is converted to digital (ie, the number of acquisitions per second). The higher the frequency, the more signal acquisition per unit of time, and the more information is retained in the signal. Loss of information is small, the converted digital quantity can accurately reflect the value of the signal, and then the LCD display can more accurately and completely display the signal waveform. The more sampling points, the more points are displayed and the clearer it is.
There are at least two parts to a digital oscilloscope: the Y channel and the sampling part of the signal being measured. The Y channel amplifies (or attenuates) the signal under test. The bandwidth is for the Y channel. If the Y channel can amplify all sinusoidal signals in the 0-10 MHz range without distortion, its bandwidth is 10 MHz. Since the signals of complex waveforms are composed of sinusoidal signals of various harmonics and the bandwidth of these harmonics may be very wide, in order to ensure the real amplification of complex signals, the larger the bandwidth of your Y channel, the better.
Only the Y-channel with enough bandwidth is not enough. In order to capture the waveform, you have to sample the signal amplified by the Y-channel! The sampling speed is the sampling rate. The faster the sampling rate, the more points are captured in complex waveforms per unit of time, and the more the final assembled waveform is closer to the actual complex signal.
So, although bandwidth and sampling rate are two different parameters, they are all very important for true restoration of the measured waveform.
Copper Heat Sink,Skiving Heat Sink,Copper Ram Heatsink,Large Copper Heatsink
Original Electronics Technology (Suzhou) Co., Ltd. , https://www.original-te.com
